堆疊的抽象資料結構
在本文中,我們仍然實作堆疊,但將內部實作從串列抽換成陣列。讀者可以和我們先前的文章相比較。
堆疊的抽象資料結構如下:
S is a stack.
sub IsEmpty(S): bool
(Optional) sub IsFull(S): bool
(Optional) sub Size(S): sz
sub Peek(S): data
sub Push(S, data): void
sub Pop(S): data由這個例子可以發現,即使在不同的實作中,公開界面可以是相同的。
堆疊型態的公開界面
以下是堆疊型態的公開界面:
#ifndef STACK_H
#define STACK_H
#ifndef __cplusplus
#include <stdbool.h>
#endif
typedef struct stack_t stack_t;
#ifdef __cplusplus
extern "C" {
#endif
stack_t * stack_new(void);
void stack_delete(void *self);
bool stack_is_empty(const stack_t *self);
int stack_peek(const stack_t *self);
bool stack_push(stack_t *self, int data);
int stack_pop(stack_t *self);
#ifdef __cplusplus
}
#endif
#endif /* STACK_H */如果和前一篇文章比較,可以發現公開界面是相同的。在實作程式時,公開界面和內部實作是分開。在不更動公開界面的前提下,改善內部實作,就是對程式碼重構 (refactoring)。
宣告堆疊類別
以陣列為基礎的堆疊的內部如下:
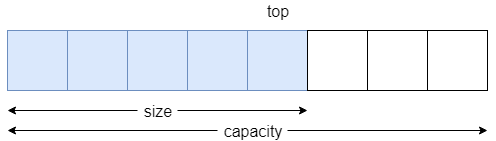
在這個堆疊陣列中,隱含著兩個長度,size 表示堆疊當下的大小,capacity 表示堆疊的最大容量。另外 top 是陣列的索引 (index),指向堆疊的頭端。
以陣列實作堆疊時,型態宣告如下:
typedef struct stack stack_t;
struct stack {
size_t size;
size_t capacity;
size_t top;
int *elements;
};我們會在類別中儲存兩個堆疊大小的資訊,size 是目前的堆疊大小,capacity 則是堆疊的最大容量。由於我們使用環狀陣列,top 所指向的位置會移動,top 使用索引值取代指標來指向堆疊的頂點。
堆疊的建構函式
以 C 語言實作堆疊的建構子如下:
stack_t * stack_new(void)
{
stack_t *s = malloc(sizeof(stack_t));
if (!s)
return s;
s->size = 0;
s->capacity = 2;
s->top = 0;
s->elements = malloc(s->capacity * sizeof(int));
if (!(s->elements)) {
stack_delete(s);
s = NULL;
return s;
}
return s;
}在此處的 s->capacity 的值可設為任意大於等於 2 的值,一開始時通常會先預先配置某個大小的容量,像是 16 或 32;此處故意設為 2 是要測試擴展容量的情境。
堆疊的解構函式
以下是 C 語言的解構函式:
void stack_delete(void *self)
{
if (!self) {
return;
}
int *elements = ((stack_t *) self)->elements;
if (elements)
free(elements);
free(self);
}要先釋放堆疊內部的陣列後再釋放堆疊物件本身。由於內部陣列是整塊的記憶體,可以直接把整塊記憶體釋放掉,不需使用迴圈。
檢查堆疊是否為空
以下是 IsEmpty(S) 的 C 程式碼:
bool stack_is_empty(const stack_t *self)
{
assert(self);
return self->size == 0;
}利用陣列大小來檢查堆疊是否為空即可。
檢視堆疊頂端的資料
以下是 Peek(S) 的 C 程式碼:
int stack_peek(const stack_t *self)
{
assert(!stack_is_empty(self));
return self->elements[self->top];
}以陣列實作堆疊時,top 是一個整數,作為陣列索引值,用來取代指標,指向堆疊的頂點。
將資料推入堆疊頂端
當我們要堆入節點時,要先將 top 移動到下一個節點所在的位置:

接著推入新的資料節點即可:

細心的讀者可能會想到堆疊容量滿出來的情境,其實我們會在推入資料節點前預先擴展堆疊陣列,詳見下文。
以下是 Push 的 C 語言實作:
bool stack_push(stack_t *self, int data)
{
if (!stack_expand(self))
return false;
if (stack_size(self) > 0)
self->top = (self->top + 1) % self->capacity;
self->elements[self->top] = data;
self->size++;
return true;
}我們在要推入元素前,會先檢查堆疊是否已滿,若堆疊容量已達上限,則擴充容量;下文會再說明 stack_expand() 部分的程式碼。我們將 top 推移後塞入 data 並將 size 遞增 1,在這裡採用環狀陣列,故 top 的值要用環狀平移來處理。
在平移 top 時,注意我們是將 top 指向陣列的後端而非前端,故其值為加 1 而非減 1。讀者自行追蹤程式碼就知道在此處指向尾端或頭端效果是相同的,只要方向一致即可。
以下是等效的
以下是 stack_expand() 的示意圖:
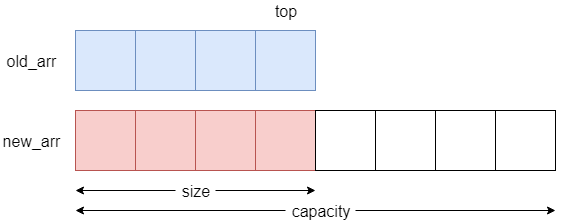
我們建立一個新的陣列,新陣列的容量為原陣列的大小的兩倍,再逐一將元素從舊陣列拷貝到新陣列即可。
以下是 stack_expand() 的 C 語言實作:
static bool stack_expand(stack_t *self)
{
if (self->size < self->capacity) {
return true;
}
int *old_arr = self->elements;
self->capacity = self->size * 2;
int *new_arr = malloc(self->capacity * sizeof(int));
if (!new_arr) {
return false;
}
size_t sz = 0;
int i = self->top;
int j = self->top;
while (sz < self->capacity) {
new_arr[i] = old_arr[j];
i = i == 0 ? self->capacity - 1 : i - 1;
j = j == 0 ? self->size - 1 : j - 1;
sz++;
}
self->elements = new_arr;
free(old_arr);
return true;
}當堆疊大小小於堆疊容量時,不需擴展容量,這時直接結束函式即可。反之,則使用環狀陣列的手法逐一複製元素。要注意 i 和 j 平移的距離相異,因為 new_arr 和 old_arr 的大小不同。
將資料移出堆疊頂端
當我們要將資料移出節點時,先將 top 節點的資料拷貝出來,再將 top 移動:

其實我們已經完成了。原本舊的 top 節點所在的資料呢?在下一次推入資料時會自動覆蓋:

以下是 Pop 的 C 程式碼:
int stack_pop(stack_t *self)
{
assert(!stack_is_empty(self));
int popped = self->elements[self->top];
self->top = self->top == 0 ? self->capacity - 1 : self->top - 1;
self->size--;
return popped;
}在本文的範例中,我們沒有縮減 (shrink) 堆疊,故只要將 top 遞移並將 size 遞減即可。由於我們的 S.top 指向陣列的尾端,故其值為減 1 而非加 1。隨著使用本範例程式的堆疊的過程,該堆疊所占的記憶體會漸增,如果很在意記憶體的消耗,可以自行嘗試實作縮減堆疊的函式。
在實作時,self->top 的型別為 size_t,該型別的值無法小於 0,故採用範例中的方式來實作環狀佇列。
演算法上的效率
以本文實作的程式效率如下:
IsEmpty(S):O(1)Peek(S):O(1)Push(S, data):amortizedO(1)Pop(S):O(1)
Push 在堆疊擴張時,程式效率為 O(n),但不是每次推入元素時都要擴張堆疊,透過攤平分析法 (amortized analysis) 可知效率為約略為 O(1)。









